
文中PA均指代并行算法。
第四章 PA的设计基础
通常,对于算法的描述使用形式化描述。提倡形式化描述是因为其严谨性、没有歧义。当然,如果算法过于复杂,使用物理描述也是可以接受的。
算法可以分为:串行算法和并行算法。这两个概念是基于硬件平台讲的。如果是执行在并行机(并且使用了多个处理器)那么就是PA(并行算法)。并行算法在此处有半形式化定义,即:
- 一些能够同时(simultaneously)执行的进程的集合
请注意,进程(或称过程,process)和处理器(processor)有区别,但当一个process运行在一个物理processor时二者也可以混为一谈。
算法的分类
请见第一篇
PA的表达
分为物理描述(就是说人话)和形式描述(类计算机语言)。形式描述语言是:
- 可以使用类Algol、类Pascal等;
- 在描述语言中引入并行语句。
- 并行语句示例:Par-do语句和for-all语句
for i=1 to n par-do
……
end for
for all Pi, where 0≤i<k
……
end for
(注:Pi可以是process或processor)
PA复杂性度量指标
算法复杂性度量使用渐进表示,上界使用big-O记号,下界使用big-Ω记号,紧致界使用big-Θ表示。这在离散数学/数据结构/算法设计与分析课程中都见过。
此外还有一些参数:
- 运行时间t(n):包含计算时间和通讯时间,分别用计算时间步和选路时间步作单位。n为输入规模。
- 处理器数p(n)
- 并行算法成本c(n)=t(n)p(n)
- 总运算量W(n)
Brent定理用于预估一个「已知耗时的串行算法」并行化后的耗时:算法A使用p台处理器可在t(n)=O(W(n)/p+T(n))时间内执行完毕(详见课件,证明在书)
PA的同步和通讯
同步:就是等待,规定在某一时间点必须全部等待最慢的完成再继续。目的是保证执行顺序的正确性。可用软件、硬件和固件的办法来实现。示例算法4.1:访问临界区之前的等待
通讯,就是互相通气。在不同的模型上使用不同原语,例如共享存储模型上的global read(X,Y)和global write(X,Y),分布存储模型上的send(X,i)和receive(Y,j)。
算法4.1 共享存储多处理器上求和算法
输入:A=(a0,…,an-1),处理器数p
输出:S=Σai
Begin
(1)S=0
(2)for all Pi where 0≤i<p do
(2.1) L=0
(2.2) for j=i to n step p do
L=L+aj
end for
(2.3) lock(S)
S=S+L
(2.4) unlock(S)
end for
End
并行计算模型(要点)
直观理解,会发现稍后介绍的全部算法都有计算模型的前提列出,比如“在SIMD-TC(SM)上的求最大值算法”。也就是算法是就模型而言的。
为什么要讲并行计算模型
- 一个算法设计出来就要在并行计算平台上运行
- 那么在算法设计之初就要考虑在哪种平台上运行
- 我们都希望一个算法设计出来是general而不是specific的
- 那么就需要把一类具体的并行计算平台抽象成为一组参数
并行计算模型的三要素
- 参数(parameter)
- 若干个能反映计算特性,且可测量/可计算的一组数据
- 什么样的数据?——影响算法的性能参数。(剧透:如果没有n/2个processor,那么求最大值算法的复杂度就无法达到logn)
- parameter举例:处理器个数、IO能力、网络带宽、存储器容量、CPU性能……
- parameter作用:构造cost function
- 有了parameter,就可以抛开总线连接方式、寄存器个数…等体系架构师所关注的细节问题。就能将精力聚焦于算法的构想
- 计算行为(behavior)
- 是同步?异步?分相?分超级步?
- 开销函数(cost function)
- 由parameter和behavior共同得出
所以并行计算模型是算法设计者与体系架构师之间的桥梁。
第一代:SM
PRAM(SIMD-SM)
有一个集中的共享存储器和一个指令控制器,通过SM的R/W交换数据,隐式同步计算。显然存在竞争,故有以下分类:
- PRAM-CRCW 性能最高
- CPRAM-CRCW(Common PRAM-CRCW):仅允许写入相同数据
- PPRAM-CRCW(Priority PRAM-CRCW):仅允许优先级最高的处理器写入
- APRAM-CRCW(Arbitrary PRAM-CRCW):允许任意处理器自由写入
- (quick sort算法的并行化就用到了这个特性)
- PRAM-CREW
- PRAM-EREW
它们之间的关系:PRAM-CRCW是最强的计算模型,PRAM-EREW可logp倍模拟PRAM-CREW和PRAM-CRCW
该模型优点是适合并行算法表示和复杂性分析,基于此模型出现了一大波脍炙人口的并行算法。缺点是不适合MIMD并行机,忽略了SM的竞争、通讯延迟等因素
异步APRAM(MIMD-SM)
也称为分相(Phase)PRAM。分相,相就是phase,被同步路障分隔开的就是phase1、phase2等。
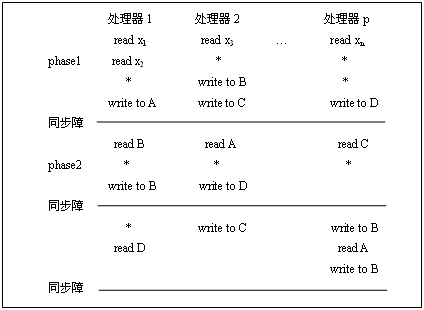
每个处理器有其局部存储器、局部时钟、局部程序;无全局时钟,各处理器异步执行;处理器通过 SM(共享存储) 进行通讯;处理器间依赖关系,需在并行程序中显式地加入同步路障。
计算过程:由同步障分开的phase1、phase2等组成
特点:不同处理器相内异步,相间设置同步路障
APRAM上的计算时间为:
T=\sum t_{p h}+B \times \text { 同步障次数 }
优点是易编程和分析算法的复杂度。缺点是与现实相差较远,其上并行算法非常有限,也不适合MIMD-DM模型。
第二代:DM
BSP(异步MIMD-DM)
由Valiant(1990)提出的。显式的「块」同步,将计算划分为多个“super step”,每个“super step”内允许异步计算和通信,但所有处理器必须在“super step”结束时通过全局同步。同步通过send-recv。图片是一个“super step”的情形。可以脑部多个“super step”竖着罗列起来(和APRAM没什么区别)

通过三个参数抽象计算与通信的分离,强调批量通信与同步的平衡,适合粗粒度并行任务(如大规模图处理):
- p:处理器数(带有存储器)
- l:同步时间间隔(Barrier synchronization time)
- g:带宽因子(time steps/packet)=1/bandwidth
计算过程:由若干“super step”组成
每个“super step”所用时间(W_i是局新计算时间,g是带宽倒数,h_i是收发消息包的个数,L是路障时问):
t=\operatorname{Max}\left(w_{i}\right)+\operatorname{Max}(h_{i}, g)+L
假设一共s个“super step”,那么总时间为:
T_{B S P}=\sum_{i=0}^{s-1} w_{i}+g \sum_{i=0}^{s-1} h_{i}+s L
LogP
LogP为啥叫LogP,是四个参数的首字母:
- L:network latency
- o:communication overhead
- g:带宽因子,同BSP的
- P:processors个数
- 注:L和g反映了通讯网络的容量
跟BSP比就是变成了点到点通讯,开销固定为2o+L(o是overhade,不是二十),隐藏了并行机的网络拓扑、路由、协议。
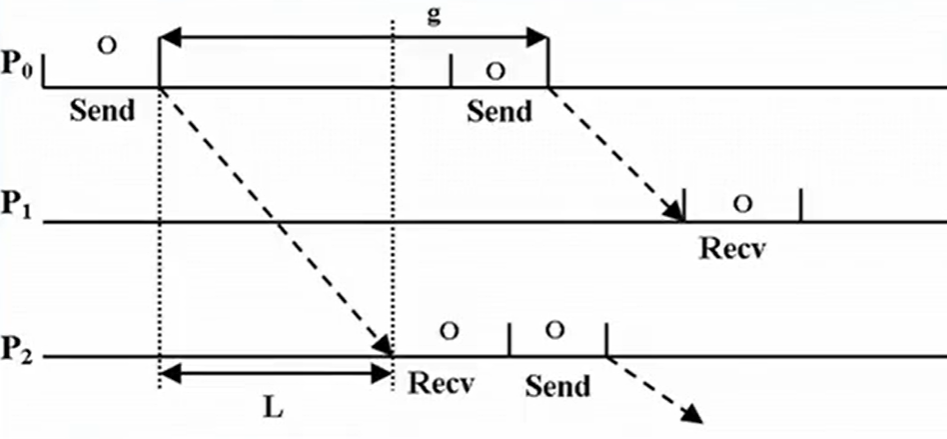
BSP vs. LogP 见课件。反正就是LogP不再被使用了。
第三代:Hierarchical
分布式共享。这里老师让脑补了一个图。画出来大概是这样的:
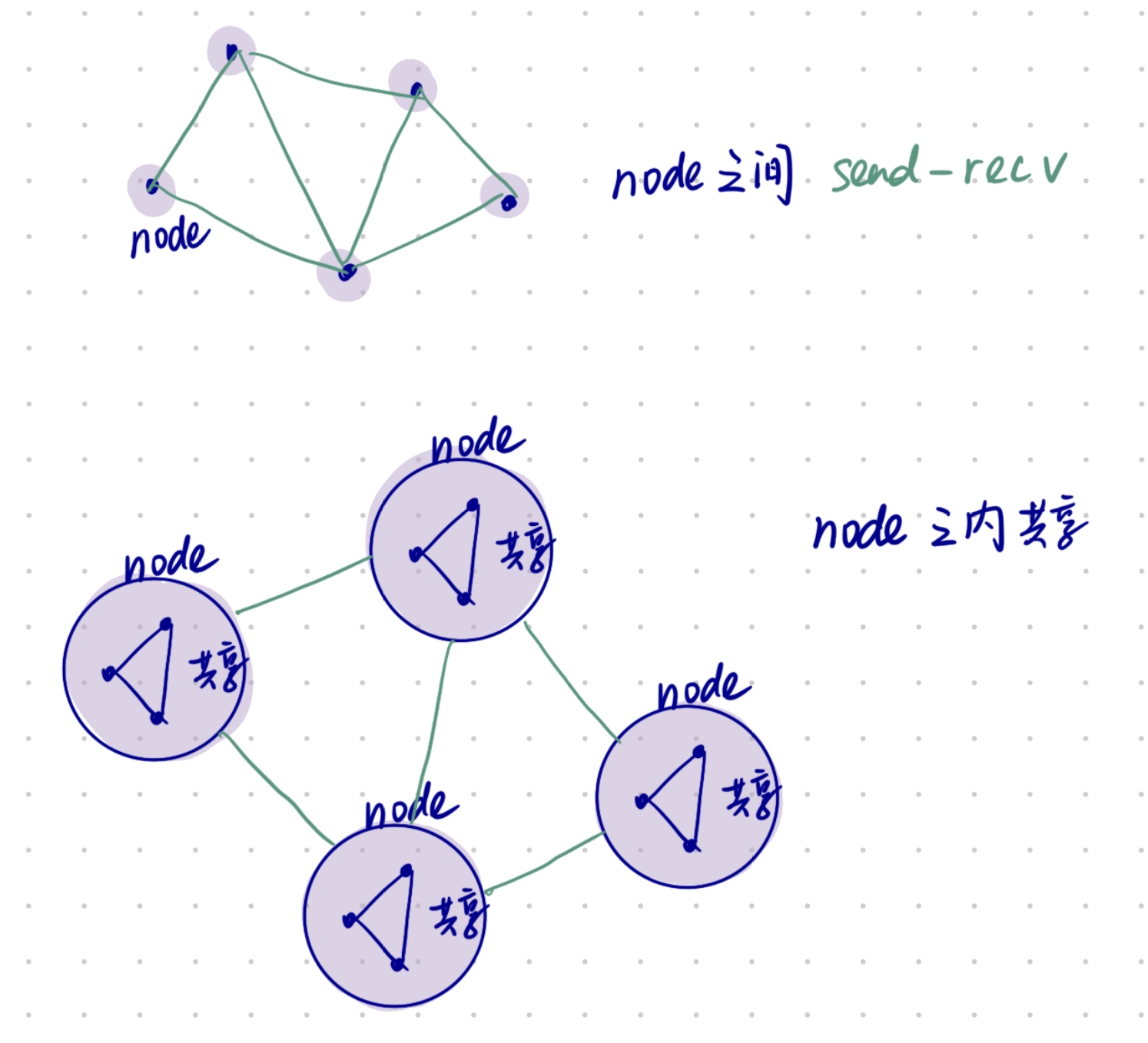
模型的发展并不是空谈,而是被体系结构的发展所推动的。
这个还是比较难定义的,要想清楚:
- 哪些参数能反映存储器层次化。
- 行为是什么?
- 开销函数怎么定义?
- 难点:访问同一层次级别(比如cache)的时间是不一样的(命中/不命中)。
发展中的模型(指2006年):
- UMH
- Memory-logP
- 不要提出新模型,把之前的修正一下继续用,Memory就代表考虑了存储器层次化
- DRAM(h,k)1
- 张云泉,串行模型,基于RAM模型,处理器i在k层次的访问时间

它们的共同点是,对于难以精细化考虑的东西,就将其简化。比如认为访存时间是固定的。
第五章 PA的一般设计方法
方法一:串行算法的直接并行化
– 有效
– 大部分
– 发掘和利用现有串行算法中的并行性,直接将串行算法改造为并行算法
例子:quick sort的并行化
Begin
(1)for each processor i do
(1.1)root=i
(1.2)fi=root
(1.3)LCi=RCi=n+1
end for
(2)repeat for each processor i<>root do
if (Ai<Afi) ∨ (Ai=Afi ∧ i<fi) then
(2.1)LCfi=i
(2.2)if i=LCfi then
exit
else
fi=LCfi
endif
else
(2.3)RCfi=i
(2.4)if i=RCfi then
exit
else
fi=RCfi
endif
endif
end repeat
End
方法二:从问题描述开始设计PA
方法三:借用已有(并行)算法求解新问题
– 新问题和原问题长得越不像,这种贡献就越大。
– 使用矩阵乘法算法求解所有点对间最短路径是一个很好的范例。
例子:矩阵乘法求解点对最短路
- 对偶
- 乘法→加法
- 求和→求min
第六章 PA的基本设计技术(要点)
划分设计技术
分为均匀/方根/对数/功能划分。前三个类似。
均匀划分技术
面向例子学习。
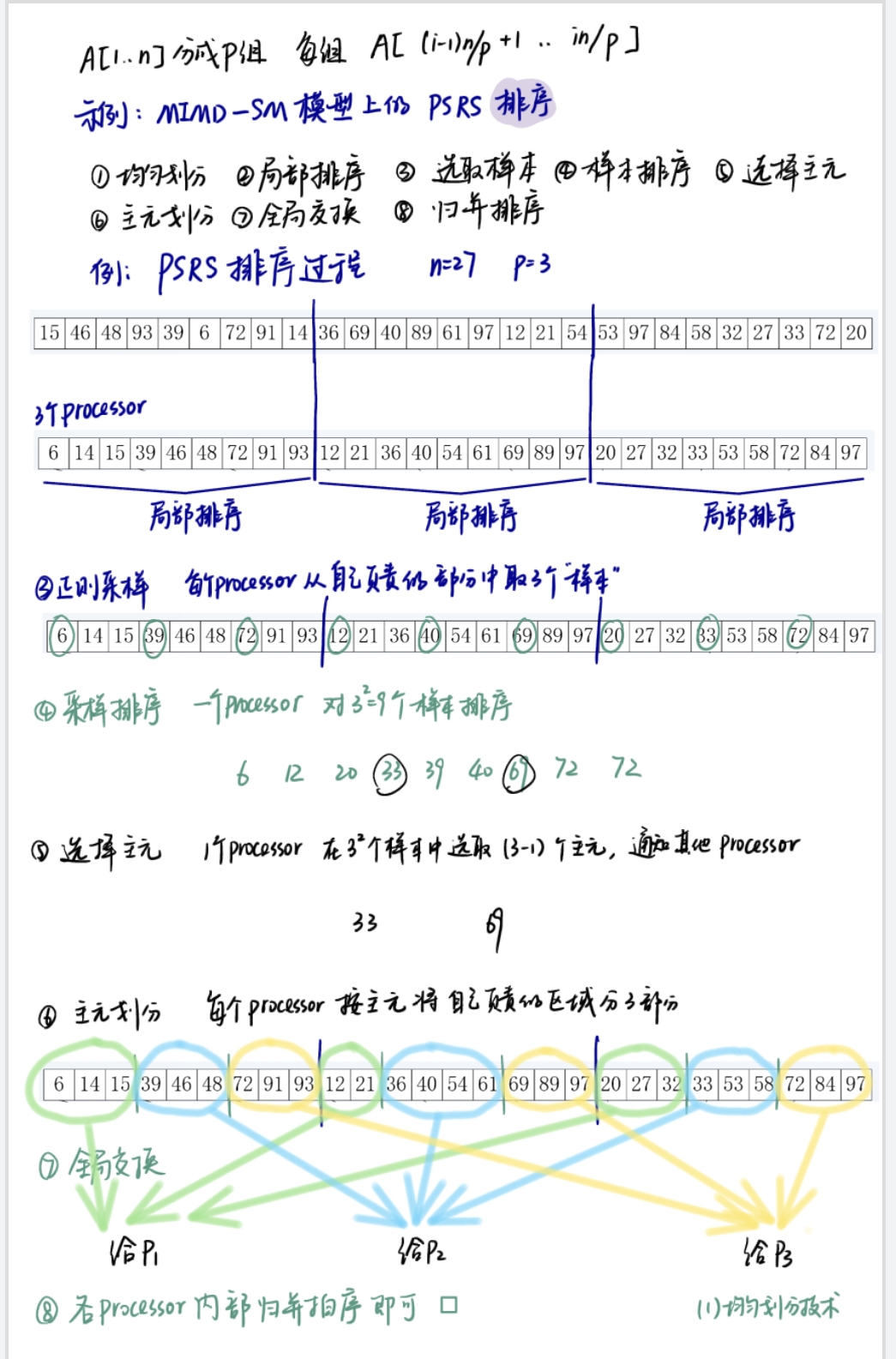
方根划分技术
面向例子学习。

约定是短的归并到长的。
Valiant归并算法时间复杂度讨论:
记 \lambda_{\mathbf{i}} 是第 \mathbf{i} 次递归后的 \mathbf{A} 组最大长度, \Rightarrow\lambda_{0}=p \lambda_{i} \leq\left\lfloor \sqrt{\lambda_{i-1}}\right\rfloor \leq \cdots \leq\left \lfloor p^{2^{-i}}\right\rfloor
算法在 \lambda_{i}= 常数 C 时终止递归,即 \left\lfloor p^{2^{-}}\right\rfloor \geq 常数 C \Rightarrow i \leq \log \log p+ 常数 C_{1}
算法中其他各步的时间为 O(1) ,所以 Valiant 归并算法时间复杂度为:
t_{k}(p, q)=O(\log \log p) \quad p \leq q
对数划分技术
讲的不细,反正就是比方根划分得还细,对处理器数量要求还要高。方根划分已经最平衡时间开销与处理器个数了,都是根号级别的嘛。
功能划分技术
在100个数里选出m个最小的。把100个数分为每m个一组,此时显然哪个也不能扔掉。但如果每两组进行比较,就能直接干掉一半。以此类推。
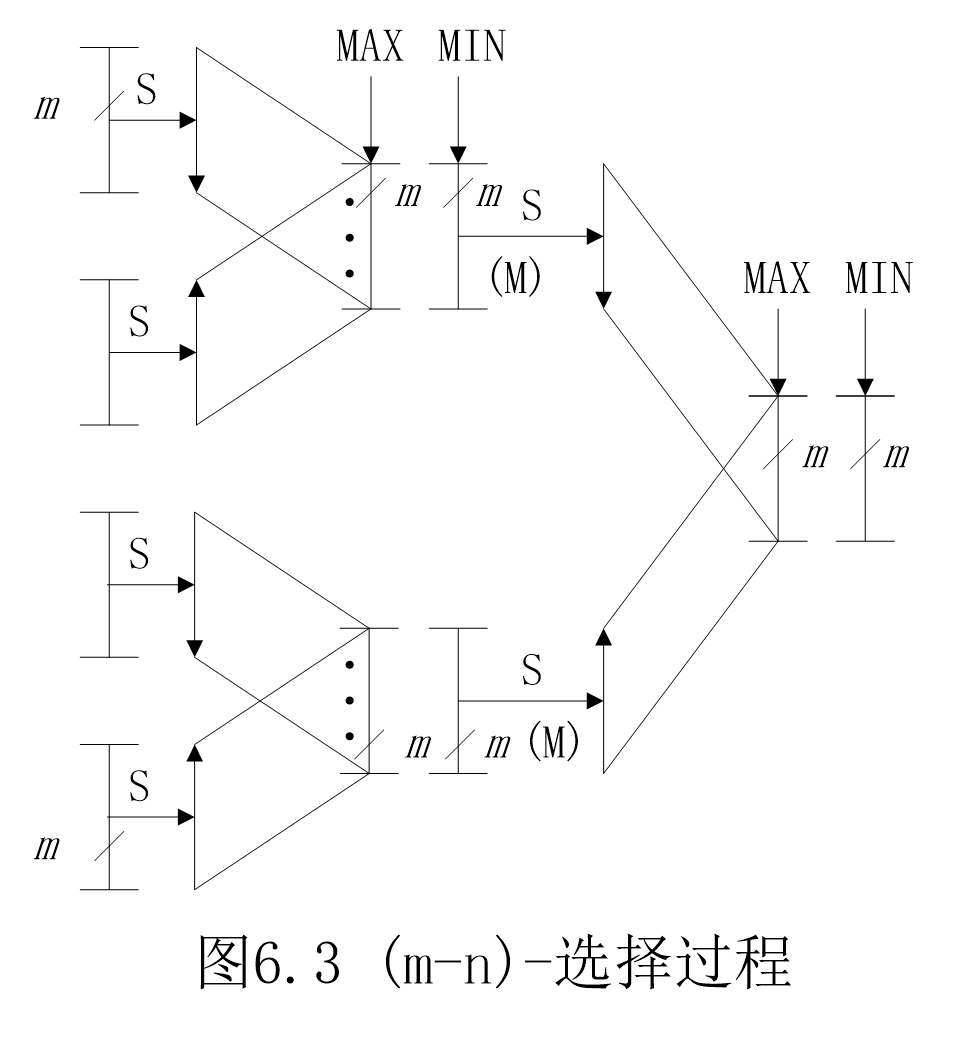
分治设计技术
并行分治设计步骤
- 将输入划分成若干个规模相等的子问题;
- 同时(并行地)递归求解这些子问题;
- 并行地归并子问题的解,直至得到原问题的解。
双调归并网络(略)
双调序列
– 调,分为升调和降调。
– 双调,就是一个序列里有两个有序的子段。
– 比如1,3,5,7,8,6,4,2,0
双调归并网络,是一种比较器网络
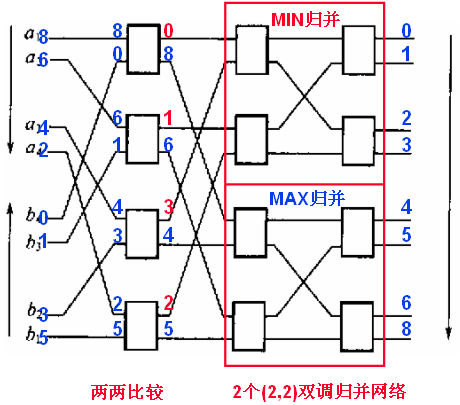
banyan网!!?
平衡树设计技术
以树的叶结点为输入,中间结点为处理结点,由叶向根或由根向叶逐层进行并行处理。
求最大值
- 不插图了,脑补一下一棵二叉树
- t(n) = O(logn)
- p(n) = n/2
计算前缀和
- 串行算法的时间复杂度是O(n)
- 如果学过竞赛就会认出它是树状数组
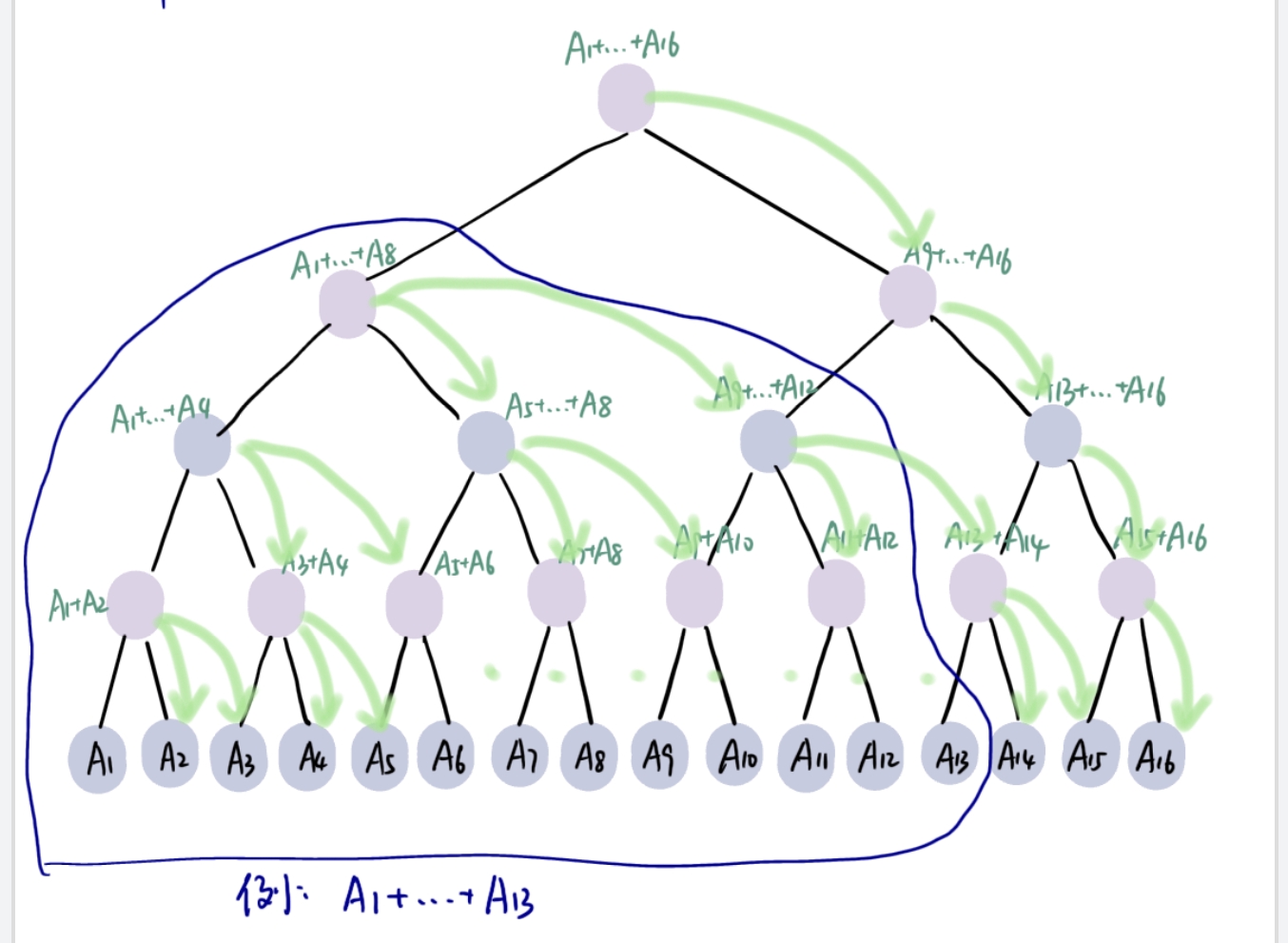
倍增设计技术
或称指针跳跃技术,特别适合于处理链表或有向树之类的数据结构。
当递归调用时,所要处理数据之间的距离逐步加倍,经过k步后即可完成距离为2k的所有数据的计算。
表序问题
问题描述:在链表上求出每个节点到表尾的跳数
还是看图面向例子学习。
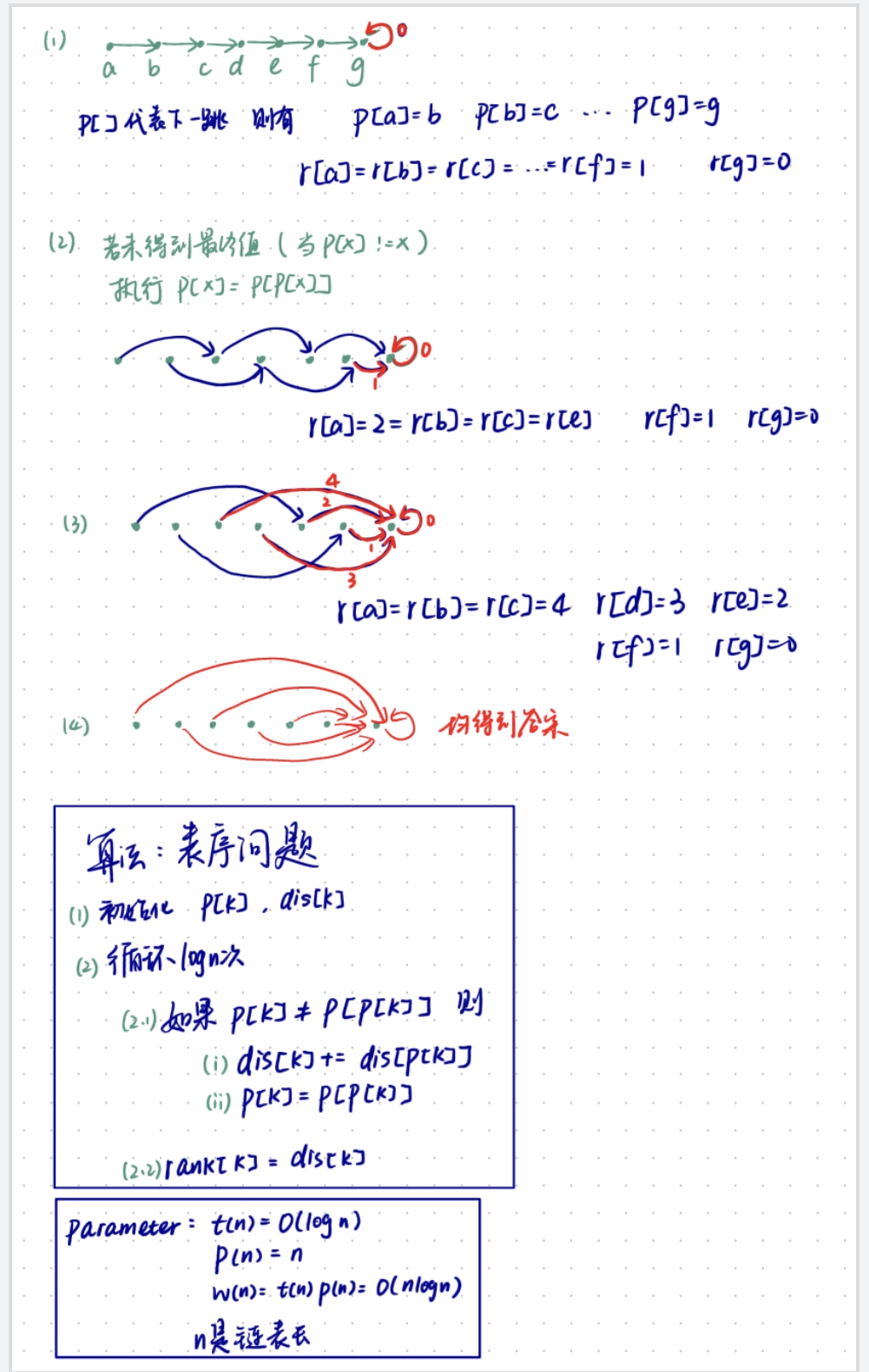
求森林的根
思路同表序问题。parameter和复杂度分析也一样。
流水线设计技术(略)
看不懂什么傅里叶 (⌒_⌒; )
第七章 PA的一般设计过程
类似于软件工程,讲一般的设计流程。但是伟大算法不是大佬一拍脑门想出来的吗(⌒_⌒; )
课外阅读:
1. 6分钟红色纪录片《我国非数值并行计算的推广——陈国良》https://dl.ccf.org.cn/video/videoDetail.html?id=5531122082859012