论文翻译
一种分布式最小权重生成树算法(R. G. GALLAGER, P. A. HUMBLET, and P. M. SPIRA 麻省理工学院)
分类和主题描述符:网络架构与设计—分布式网络;非数值算法与问题;图论—树 关键词:算法,分布式算法,通信复杂度,最短生成树
摘要
本文提出了一种分布式算法,用于在具有互异边权重的连通无向图中构建最小权重生成树。图的每个节点处存在一个处理器,各处理器最初仅知晓相邻边的权重。这些处理器遵循相同的算法,并与邻居交换消息,直到生成树构建完成。对于一个具有 N 个节点和 E 条边的图,所需的消息总数最多为 5N \log_2 N + 2E,且每条消息最多包含一个边权重以及 \log_2 8N 位信息。该算法可以在任何节点或任何节点子集上自发启动。
1 引言
在本文中,我们考虑一个具有 N 个节点和 E 条边的连通无向图,其中每条边都被赋予了一个互不相同的有限权重。我们描述了一种异步分布式算法,该算法能够确定该图的最小权重生成树。我们假设每个节点最初只知道与该节点相邻的各条边的权重。
每个节点执行相同的本地算法,该算法包括通过相邻链路发送消息、等待接收传入消息以及进行处理。消息可以在一条边上独立地双向传输,并在经历不可预测但有限的延迟后无误且按序到达。在每个节点完成其本地算法后,它知道哪些相邻边位于生成树中,并且也知道哪条边通向被指定为树核心的特定边。
我们将图中的节点视为最初处于睡眠状态。然后,一个或多个节点自发地或在接收到来自已唤醒邻居的消息后唤醒,并随后执行其本地算法。
在这些假设下,我们将看到,节点之间为找到 MST 而交换的消息总数少于 2E + 5N \log_2 N。每条消息最多包含一个边的权重、一个介于零和 \log_2 N 之间的整数以及三个附加位。
我们的算法类似于 Spira [8] 早前描述的一种算法,而该算法又遵循了 Dalal [1] 提出的更早的算法。Spira 没有详细分析其算法所需的消息数量,但他给出了一个启发式论证,表明(在随机选择的图上)预期消息数量将随 E 和 N 的增长率为 E + N \log N。
如果网络节点具有可排序的互异标识,那么很容易将算法扩展到边权重不唯一的情况。只需将连接该边的两个节点的标识附加到边权重上,例如,先列出排序较低的节点。这些附加后的权重具有与之前相同的顺序,平局则由节点标识来打破。如果节点不知道其邻居的标识,那么每个节点可以通过每条相邻边发送其标识,这总共需要 2E 条额外消息。我们还开发了另一种算法(稍后简要描述),它不需要唯一的权重,因此也不需要这些额外的 2E 条消息。
如果网络既没有唯一的边权重,也没有唯一的节点标识,那么不存在任何分布式算法(如上所述的类型)能够以有限数量的消息找到 MST。这一点在一个三节点全连接且边权重相等的图中最容易看出。任意两条边都可以构成一个 MST,但由于节点遵循相同的算法,它们无法进行选择。如果节点选择随机标识,那么一旦所有标识都不同,算法就可以工作,但无法保证在有限次选择内实现这一点。自然,所需的预期选择次数很少,但任何有限数量的消息都会以某个正概率失败。
分布式 MST 算法在通信网络中非常有用,特别是当需要将信息从一个节点广播到所有其他节点,并且网络的每个信道都存在关联成本时。如果在一个方向上使用信道的成本与相反方向不同,那么 MST 不能提供所需的解决方案,但一篇姊妹论文 [3] 处理了这个更普遍的问题。除了广播应用之外,对于许多网络控制问题,如果已知一个生成树,其通信复杂度可以降低。由于网络中可能的故障会导致拓扑变化,因此需要能够从任何节点或节点子集开始生成一个生成树,而本文的算法在生成任意生成树方面与我们能找到的任何其他算法一样高效。最后,分布式算法还有许多应用,例如可以选择网络中具有最高标识号的节点。解决该问题的一种高效分布式算法始于 MST 算法,然后使用生成的树来寻找编号最高的节点。
2 生成树回顾
我们假设读者熟悉图、路径、环、树等的基本定义和性质,这些内容可以在例如[5, 6]中找到。假设图的每条边 e 都有一个关联的权重 w(e)。图中一棵树的权重定义为其所有边的权重之和,而我们的目标是找到一棵具有最小权重的生成树,即最小权重生成树(MST)。MST的一个片段 定义为该MST的一棵子树,即该MST的一个连通节点和边集。该算法开始时,每个单独的节点作为一个片段,最终整个MST作为一个片段结束。定义一条边为片段的出边,如果该边的一个邻接节点在片段内,而另一个不在。
性质 1. 给定一个MST的片段,令 e 为该片段的一条最小权重出边。那么将 e 及其邻接的非片段节点加入该片段,将得到另一个MST的片段。
证明. 假设添加的边 e 不在包含原片段的MST中。那么由 e 和MST边的某个子集会形成一个环。该环中至少有一条边 x \neq e 也是该片段的出边,因此有 w(x) \geq w(e)。因此,从MST中删除 x 并添加 e 形成了一棵新的生成树,如果原树是最小的,那么新树也必然是最小的。添加了 e 的原片段是新MST的一个片段。□
性质 2. 如果连通图的所有边都具有不同的权重,那么其MST是唯一的。
证明. 反证法,假设存在两个不同的MST。令 e 为存在于其中一个但不同时存在于两个树中的最小权重边,并令 T 为包含 e 的MST的边集,T’ 为另一个MST的边集。边集 {e} \cup T’ 必然包含一个环,并且该环中至少有一条边,记为 e’,不在 T 中(因为 T 不含环)。由于所有边的权重都不同,且 e’ 只存在于一个树中而非两个树中,故有 w(e) \lt w(e’)。因此, {e} \cup T’ – {e’} 是权重小于 T’ 的生成树的边集,这与假设矛盾。□
这些性质立即为具有不同边权重的图寻找MST提出了一类通用算法。可以从一个或多个由单个节点组成的片段开始。利用性质1,可以按任意顺序扩展这些片段。每当两个片段有一个公共节点时,性质2向我们保证这些片段的并集也是一个片段,从而允许片段合并成更大的片段。生成MST的标准算法对应于上述片段扩展和合并的不同顺序。例如,Prim-Dijkstra算法[2, 7]从单个节点开始,连续扩展该片段直到它覆盖整个图。Kruskal算法[4]从所有节点作为片段开始,连续扩展具有最小权重出边的片段,并在可能时合并片段。其他算法[1, 8, 9]从所有节点作为片段开始,扩展每个片段,然后合并,接着扩展每个新的扩大后的片段,再次合并,依此类推。
如果某些边权重相同,Prim-Dijkstra算法和Kruskal算法同样适用。要理解这一点,只需在算法执行过程中所做选择的基础上,对等权边施加一个一致的任意顺序。像[1], [3]和[9]这样没有中间合并步骤而扩展多个片段的算法,在边权重相等时不一定能正确工作。例如,在一个三节点全连接网络且边权重相等的情况下,每个节点可能通过不同的边进行扩展,从而在合并片段时产生环。
在接下来的算法中,每个片段独立于其他片段异步地寻找其最小权重出边,并且当找到该边时,该片段尝试与位于该边另一端的片段合并。合并的方式和时间取决于两个片段的层级,而层级又取决于之前的片段合并。具体来说,包含单个节点的片段被定义为层级0。假设一个给定的片段 F 处于层级 L \geq 0,并且位于 F 的最小权重出边另一端的片段 F’ 处于层级 L’。如果 L \lt L’,则片段 F 立即作为片段 F’ 的一部分被吸收,扩展后的片段处于层级 L’。如果 L = L’ 且片段 F 和 F’ 具有相同的最小权重出边,则这两个片段立即合并成一个新的层级为 L + 1 的片段;该合并边随后被称为新片段的核心(core)。在所有其他情况下,片段 F 只是等待,直到片段 F’ 达到足够高的层级以便根据上述规则进行合并。
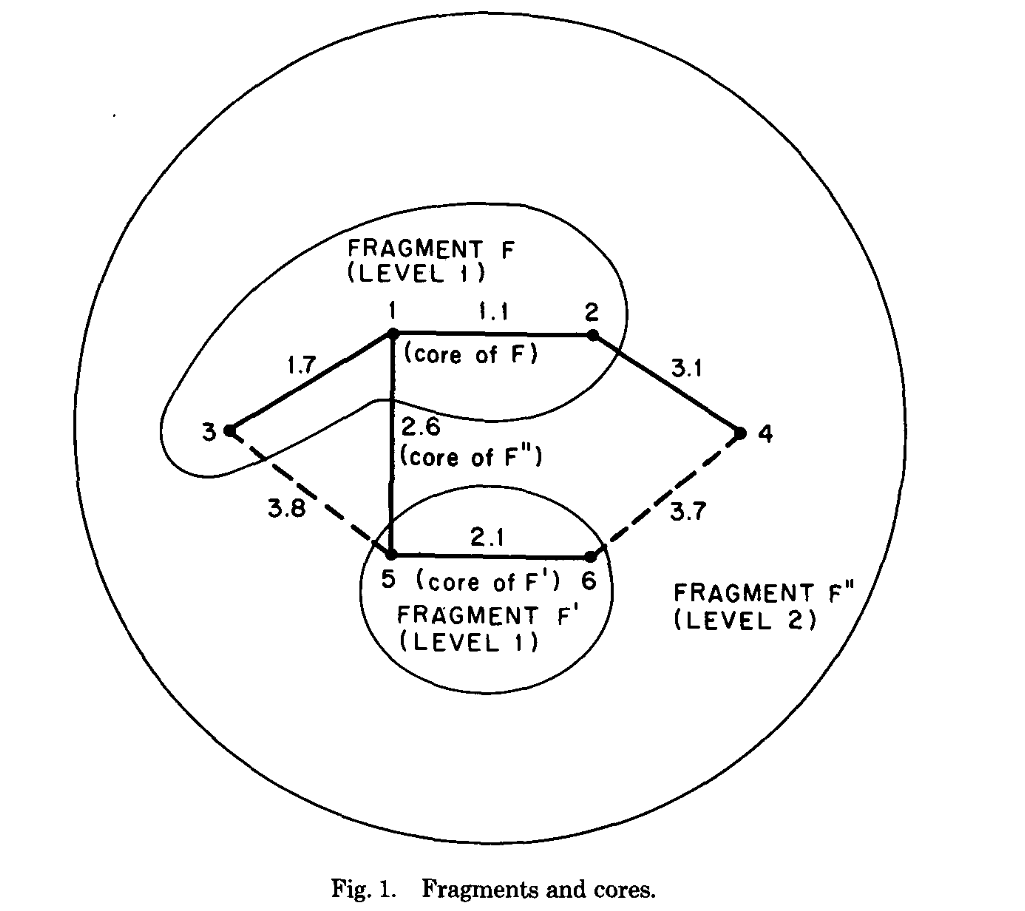
图1说明了这些规则。片段 F 是一个层级1的片段,由节点1和2在它们共同的最小权重边上合并形成,然后节点3及其最小权重边被吸收。片段 F 和 F’ 后来在它们的最小权重边上合并,形成一个层级2的片段,随后节点4被吸收。根据时间安排,节点4也可能在层级2片段形成之前被吸收到片段 F 中。
我们将在描述更多算法细节后说明,上述规则中的等待不会导致死锁。等待的原因在于,一个片段寻找其最小权重边所需的通信量与该片段的大小成正比,因此,让小片段加入大片段而不是反过来,可以减少通信量。
3 分布式算法描述
我们首先描述一个片段如何找到其最小权重出边。首先考虑零级片段(即单个节点)这个简单特殊情况。最初,每个节点处于一种称为睡眠的静止状态。节点有三种可能的状态:初始状态 Sleeping,在参与片段搜索最小权重出边时的 Find 状态,以及其他时候的 Found 状态。当一个睡眠节点自发唤醒以启动整个算法,或者因接收到来自另一个节点的任何算法消息而被唤醒时,该节点首先选择其权重最小的相邻边,将此边标记为 MST 的一个分支,沿着此边发送一条称为 Connect 的消息,然后进入 Found 状态,等待来自所选边另一端片段的响应。
现在考虑非零级片段中的节点如何协作以找到最小权重出边。假设一个层级为 L 的新片段刚刚由两个层级为 (L – 1) 的片段通过它们相同的最小权重出边合并而成,该边成为新片段的核心。该核心边的权重被用作该片段的标识。
与核心相邻的两个节点通过向片段中的其他节点广播一条 Initiate 消息来启动新的周期。该消息沿着片段的分支向外发送,并由片段中的中间节点向外转发。Initiate 消息携带新的片段层级和标识作为参数,为片段中的所有节点提供此信息。Initiate 消息还包含参数 Find,该参数将节点置于 Find 状态,如下文所述。如果其他层级为 (L – 1) 的片段正等待连接到新的层级 L 片段的节点,Initiate 消息也会传递给它们,使它们加入新片段。Initiate 消息还会传递给正等待连接到这些新节点的层级 (L – 1) 片段,依此类推。
当节点收到此 Initiate 消息时,它开始寻找其最小权重出边。这里的困难在于节点不知道哪些边是出边。这个问题通过以下方式解决:每个节点将其每条相邻边分类为三种可能状态之一:Branch,如果该边是当前片段中的一个分支;Rejected,如果该边不是分支但已被发现连接了片段的两个节点;以及 Basic,如果该边既不是分支也不是已拒绝边。
为了找到其最小权重出边,节点选择权重最小的 Basic 边,并向其发送一条 Test 消息。Test 消息携带片段标识和层级作为参数。当节点收到这样的 Test 消息时,它会检查自身的片段标识是否与 Test 消息中的标识一致。如果标识一致,那么(除一个小例外)该节点会向 Test 消息的发送者返回一条 Reject 消息,并且两个节点都将该边置于 Rejected 状态。发送 Test 消息的节点随后通过测试其下一个最佳边来继续。上述例外是,如果一个节点在同一条边上发送并随后接收到具有相同标识的 Test 消息,它会直接拒绝该边而不发送 Reject 消息;这略微降低了通信复杂度。
如果接收 Test 消息的节点的片段标识与 Test 消息中的不同,并且接收节点的片段层级大于或等于 Test 消息中的层级,那么它会向发送节点返回 Accept 消息,证明该边是发送节点所在片段的一条出边。另一方面,如果接收节点的片段层级低于 Test 消息中的层级,则接收节点将延迟做出任何响应,直到其自身层级增加到足够高。此延迟特性的主要原因是,在一个较低层级的片段合并到一个较高层级的片段之后,该片段的出边节点需要经过一段不确定的时间(实际上,直到它们收到新的 Initiate 消息)才能获知此变化。 该算法的一个重要性质是,节点的片段标识当且仅当层级增加时才会改变 ;此外,一个给定的片段标识只能出现在一个层级。这些性质从前面关于片段如何合并的讨论中可以直观地看出,并且可以通过对算法中任何允许的事件时间顺序进行归纳来严格建立。从片段的这些性质中,我们看到,当节点 A 响应 B 的 Test 消息而发送 Accept 消息时,A 的片段标识与 B 当前的片段标识不同,并且将继续保持不同。
高层级 accept 低层级 是没问题的:高层级节点信息更全、更稳定,可以立即做决定。
低层级 accept 高层级 是有潜在问题的(环路):低层级节点可能被高级节点合并,但此时消息并未传到低级的那个收到test的节点,它如果当时的片段标识不同,也许是因为消息还没同步过来,这就可能导致形成环路。等自己“升级”到与对方同级或更高级别,获取了最新信息后,才能做出可靠的判断。
—— 在GHS算法中,层级不仅仅是一个数字,它实际上充当了分布式系统中的一种”逻辑时钟”,记录了片段经历的合并历史。
我们刚刚描述了片段中的每个节点最终如何找到其最小权重出边(如果存在的话)。节点现在必须通过发送 Report 消息进行协作,以找到整个片段的最小权重出边;如果没有节点有出边,则算法完成,该片段就是 MST。具体来说,片段的每个叶子节点(即仅与一个片段分支相邻的节点)在其入向分支上发送消息 Report(W);W 是该节点最小权重出边的权重,如果没有出边,则 W 为无穷大。类似地,片段中的每个内部节点等待,直到它既找到了自己的最小权重出边,又在所有出向片段分支上收到了消息。然后,该节点将这些权重中最小的权重 W 所对应的边(或者是出边,或者是出向片段分支)记为 best-edge,并在其入向分支上发送 Report(W)。当节点发送 Report 消息时,它也进入 Found 状态,表示它在该片段寻找最小权重出边的过程中扮演的角色已完成。最终,与核心相邻的两个节点在核心分支本身上发送 Report 消息,使得这两个节点中的每一个都能确定最小出边的权重以及该边位于核心的哪一侧。
在两个核心节点交换了 Report 消息之后,片段节点保存的最佳边使得能够追踪从核心到拥有最小权重出边的节点的路径。然后,沿着该路径的每个分支发送 Change-core 消息,并且这些节点中每一个的入向边被更改为对应于 best-edge。当此消息到达具有最小权重出边的节点时,入向边形成了一棵以该节点为根的有根树。最后,该节点沿着最小权重出边发送消息 Connect(L);L 是片段的层级。
如果两个层级为 L 的片段具有相同的最小权重出边,则每个片段都沿着该边发送 Connect(L) 消息,每个方向一条,这将导致该边成为一个层级为 (L + 1) 的片段的核心,并导致携带新层级和片段标识的新 Initiate 消息被发送出去。这条形成新片段的规则确保一个层级为 (L + 1) 的片段总是包含至少两个层级为 L 的片段(L ≥ 0);由此可知,层级为 L 的片段至少包含 2^L 个节点,因此 \log_2 N 是片段层级的上界。
最后,考虑当来自一个低层级片段(层级为 L,标识为 F)中节点 n 的 Connect 消息到达一个高层级片段(层级为 L’,标识为 F’)中的节点 n’ 时会发生什么。
根据我们绝不让低层级片段等待的策略,节点 n’ 立即向 n 发送一条带有标识和层级参数 F’ 和 L’ 的 Initiate 消息。如果节点 n’ 在给定层级尚未发送其 Report 消息,则片段 F 直接加入片段 F’ 并参与寻找扩大后片段的最小权重出边。另一方面,如果节点 n’ 已经发送了其 Report 消息,那么我们可以推断出,来自节点 n’ 的一条出边的权重低于来自 F 的最小权重出边的权重。这就消除了 F 加入寻找最小权重出边搜索的必要性。这两种情况通过 Initiate 消息中发送的节点状态(Find 或 Found)来区分。片段 F 中的节点根据 Initiate 消息的这个参数进入 Find 或 Found 状态,并且它们仅在 Find 状态下发送 Test 消息。
上面这段的意思是,一个低级片段向一个高级片段发起合并请求( Connect 消息),默认是会被同意的,高级片段没有拒绝的选项。高级片段的“同意”方式是立即响应 Initiate 消息(代表你来给我干活吧,并且层级数就是L’),将低层级片段纳入自己的管辖范围。当然,“同意”之后的具体整合方式(新加入的节点进入 Find 还是 Found 状态,是要分类讨论的)
我们现在概述算法正确性的证明。考虑到性质1和性质2,只需验证算法确实能找到片段的最小权重出边,并且等待不会导致死锁。先前的算法描述应能使读者确信,在其上发送 Connect(L) 消息的边,是由所有接收到具有给定标识的 Initiate 消息的节点组成的层级 L 片段的最小权重出边(注意,对应于给定片段标识的片段可以随着低层级片段的加入而增长)。
为了证明不存在死锁,考虑在任何给定时间存在的片段集合,不包括由睡眠节点组成的零级片段。假设算法已启动但未完成,因此上述片段集合非空,并且每个片段都有一个最小权重出边。在该集合中最低层级的片段里,考虑其中一个具有最小最小权重出边的片段。来自该片段的任何 Test 消息要么将唤醒一个睡眠的零级片段,要么将在无需等待的情况下得到响应。类似地,来自该片段的 Connect 消息要么将唤醒一个睡眠的零级片段,要么将到达一个高层级片段(并立即得到 Initiate 响应),要么将到达一个具有相同最小权重出边的同层级片段,从而形成一个新的更高层级的片段。由于所假设的系统状态是任意的,我们看到不存在死锁。
附录中的程序也已经在各种网络拓扑上(使用 FORTRAN 实现)进行了测试。
我们现在简要描述算法的一个修改版本,该版本可用于非唯一的边权重,并且不需要 2E 条额外消息来将相邻节点的标识附加到边权重上。在此修改中,片段由节点标识来标识,这些节点标识是有序且唯一的。像以前一样找到片段的最小权重出边,并像以前一样在该边上发送 Connect 消息。新的特点是,如果 (1) 两个片段处于同一层级且 F > F’;(2) 某个同一层级的片段 F” 已向 F 发送了 Connect 消息且 F” \lt F;(3) 尚未在边 e 上发回 Initiate 消息,则来自片段 F 到 F’ 的边 e 上的 Connect 消息将被取消。当 Connect 消息被取消时,发送该消息的节点会增加其层级并发送新的 Initiate 消息,在这种情况下,片段 F 和 F” 合并。
附录(算法)
以下算法由每个节点遵守执行,包含了对可能生成的每种消息类型的响应列表。此外,还给出了节点自发唤醒时的响应。假定每个节点会对传入的消息进行排队,并按照先到先服务的顺序进行处理。一个特殊的响应是将消息放回队列末尾以延迟处理,但除此之外,每个响应都在开始下一个响应之前完成。当然,每个节点维护其自己的一组变量,包括其状态(记为 SN,可能取值为 Sleeping, Find, Found)、相邻边的状态。边 j 的状态记为 SE(j),可能取值为 Basic, Branch, Rejected。边的状态在边的两个相邻节点处可能暂时不一致。对于每个节点,初始状态为:对于每个相邻边 j,SN = Sleeping 且 SE(j) = Basic。每个节点还维护一个片段标识 FN、一个层级 LN,以及变量 best-edge, best-ut, test-edge, in-branch, 和 find-count,它们的初始值无关紧要。还有一个初始为空的、先到先服务的队列用于传入消息。最后,每个相邻边 j 的权重记为 w(j)。
消息:
Connect(L)
Initiate(L, F, S)
Test(L, F)
Accept
Reject
Report(w)
Change-root
算法(在每个节点执行)
(1) 事件处理:自发唤醒(只能发生在处于 Sleeping 状态的节点)
执行 wakeup()
(2) wakeup()
begin
令 m 为权重最小的相邻边;
SE(m) ← Branch;
LN ← 0;
SN ← Found;
Find-count ← 0;
在边 m 上发送 Connect(0)
end
(3) 事件处理:在边 j 上收到 Connect(L)
begin
if SN = Sleeping then 执行 wakeup();
if L < LN then
begin
SE(j) ← Branch;
在边 j 上发送 Initiate(LN, FN, SN);
if SN = Find then find-count ← find-count + 1
end
else if SE(j) = Basic then 将接收到的消息放到队列末尾
else 在边 j 上发送 Initiate(LN + 1, w(j), Find)
end
(4) 事件处理:在边 j 上收到 Initiate(L, F, S)
begin
LN ← L;
FN ← F;
SN ← S;
in-branch ← j;
best-edge ← nil;
best-ut ← ∞;
for 所有 i ≠ j 且 SE(i) = Branch 的边
do begin
在边 i 上发送 Initiate(L, F, S);
if S = Find then find-count ← find-count + 1
end;
if S = Find then 执行 test()
end
(5) test()
if 存在状态为 Basic 的相邻边
then begin
test-edge ← 权重最小的状态为 Basic 的相邻边;
在 test-edge 上发送 Test(LN, FN)
end
else begin
test-edge ← nil;
执行 report()
end
(6) 事件处理:在边 j 上收到 Test(L, F)
begin
if SN = Sleeping then 执行 wakeup();
if L > LN then 将接收到的消息放到队列末尾
else if F ≠ FN then 在边 j 上发送 Accept
else begin
if SE(j) = Basic then SE(j) ← Rejected;
if test-edge ≠ j then 在边 j 上发送 Reject
else 执行 test()
end
end
(7) 事件处理:在边 j 上收到 Accept
begin
test-edge ← nil;
if w(j) < best-ut
then begin
best-edge ← j;
best-ut ← w(j)
end;
执行 report()
end
(8) 事件处理:在边 j 上收到 Reject
begin
if SE(j) = Basic then SE(j) ← Rejected;
执行 test()
end
(9) report()
if find-count = 0 and test-edge = nil
then begin
SN ← Found;
在 in-branch 上发送 Report(best-ut)
end
(10) 事件处理:在边 j 上收到 Report(w)
if j ≠ in-branch
then begin
find-count ← find-count - 1
if w < best-ut then begin best-ut ← w; best-edge ← j end;
执行 report()
end
else if SN = Find then 将接收到的消息放到队列末尾
else if w > best-ut
then 执行 change-root()
else if w = best-ut = ∞ then 停止执行
(11) change-root()
if SE(best-edge) = Branch
then 在 best-edge 上发送 Change-root
else begin
在 best-edge 上发送 Connect(LN);
SE(best-edge) ← Branch
end
(12) 事件处理:收到 Change-root
执行 change-root()
解读
核心思想:分治合并
概念:片段fragment,核心节点u,层级L,吸收,合并,洪泛(Initiate)与回声(Report),最小出边,连接请求(Connect(L)),接收,拒绝,
- 初始化
level = 0
fragment_id = this->nodeID
state = “find”
core = this->nodeID
- 寻找本fragment的最小出边
2.1 核心节点u发起搜索(洪泛)
核心节点向片段内所有节点广播 Initiate(level, fragment_id, state)
消息沿片段树传播,每个节点更新自己的状态
2.2 每个节点本地搜索
检查所有相邻的基本边
对每条基本边发送 Test(level, fragment_id) 消息
等待对方回复 Accept 或 Reject
2.3 叶节点报告结果(回声)
叶子节点找到最小可接受边后,向父节点发送 Report(best_edge)
中间节点等待所有子节点的报告
从子节点报告和本地边中选择权重最小的边
向上传递 Report(best_edge)
最终结果汇聚到核心节点
- 片段合并
3.1 发起连接
核心确定片段的最小出边 e = (u, v)
指令节点 u 向节点 v 发送 Connect(level)
节点 v 收到后转发给所在片段的核心
3.2 合并决策
核心收到 Connect 请求后:
3.2.A 不同层级合并
低层级 → 高层级:高层级立即接受
高层级 → 低层级:低层级延迟处理
3.2.B 同层级合并
检查是否为双向选择(双方都选择对方作为最小出边)
如果是双向选择:合并并提升层级
否则:等待或拒绝
3.3 执行合并
确定新核心:连接边 (u, v) 成为新核心
新核心向两个原片段广播 Initiate(new_level, new_fragment_id, “find”)
所有节点更新状态,开始新一轮搜索